Information Centrality
Definition
This index incorporates the set of all possible paths between two nodes weighted by an information-based value for each path that is derived from theinverse of its length. Information centrality CI is defined by:
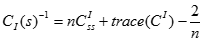 Where CI = (L+J)−1 with Laplacian L and J = 11T, and CIss is the element on the sth row and the sth column in CI. It measures the harmonic mean length of paths ending at a vertex s, which is smaller if s has many short paths connecting it to other vertices.
Where CI = (L+J)−1 with Laplacian L and J = 11T, and CIss is the element on the sth row and the sth column in CI. It measures the harmonic mean length of paths ending at a vertex s, which is smaller if s has many short paths connecting it to other vertices.
Brandes and Fleischer showed that current-flow closeness centrality is equivalent to information centrality [BRANDES, U. 2005].
See Current-Flow Closeness Centrality
See Harmonic Centrality
From 'sna' R package
Actor information centrality is a hybrid measure which relates to both path-length indices (e.g., closeness, graph centrality) and to walk-based eigenmeasures (e.g., eigenvector centrality, Bonacich power). In particular, the information centrality of a given actor can be understood to be the harmonic average of the “bandwidth” for all paths originating with said individual (where the bandwidth is taken to be inversely related to path length). Formally, the index is constructed as follows. First, we take G to be an undirected (but possibly valued) graph – symmetrizing if necessary – with (possibly valued) adjacency matrix A. From this, we remove all isolates (whose information centralities are zero in any event) and proceed to create the weighted connection matrix
See
Shan, L., Yi, Y. and Zhang, Z., 2018. Improving information centrality of a node in complex networks by adding edges. arXiv preprint arXiv:1804.06540.
Rastogi, N., 2019. Exploring Information Centrality for Intrusion Detection in Large Networks. arXiv preprint arXiv:1904.12138.
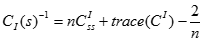
Brandes and Fleischer showed that current-flow closeness centrality is equivalent to information centrality [BRANDES, U. 2005].
See Current-Flow Closeness Centrality
See Harmonic Centrality
From 'sna' R package
Actor information centrality is a hybrid measure which relates to both path-length indices (e.g., closeness, graph centrality) and to walk-based eigenmeasures (e.g., eigenvector centrality, Bonacich power). In particular, the information centrality of a given actor can be understood to be the harmonic average of the “bandwidth” for all paths originating with said individual (where the bandwidth is taken to be inversely related to path length). Formally, the index is constructed as follows. First, we take G to be an undirected (but possibly valued) graph – symmetrizing if necessary – with (possibly valued) adjacency matrix A. From this, we remove all isolates (whose information centralities are zero in any event) and proceed to create the weighted connection matrix
C = B^-1
where B is a pseudo-adjacency matrix formed by replacing the diagonal of 1-A with one plus each actor's degree. Given the above, let T be the trace of C with sum S_T, and let S_R be an arbitrary row sum (all rows of C have the same sum). The information centrality scores are then equal to
C_I = ( T + (S_T-2S_R)/|V(G)| )^-1
(recalling that the scores for any omitted vertices are 0).
In general, actors with higher information centrality are predicted to have greater control over the flow of information within a network; highly information-central individuals tend to have a large number of short paths to many others within the social structure. Because the raw centrality values can be difficult to interpret directly, rescaled values are sometimes preferred (see the rescale option). Though the use of path weights suggest information centrality as a possible replacement for closeness, the problem of inverting the B matrix poses problems of its own; as with all such measures, caution is advised on disconnected or degenerate structures.
See
Shan, L., Yi, Y. and Zhang, Z., 2018. Improving information centrality of a node in complex networks by adding edges. arXiv preprint arXiv:1804.06540.
Rastogi, N., 2019. Exploring Information Centrality for Intrusion Detection in Large Networks. arXiv preprint arXiv:1904.12138.
Software
- CytoNCA
http://apps.cytoscape.org/apps/cytonca - JGraphT-sna
https://bitbucket.org/sorend/jgrapht-sna - NetworkX
https://networkx.github.io/ - sna
http://CRAN.R-project.org/package=sna - SocNetV
http://socnetv.sourceforge.net/ - UCINET
https://sites.google.com/site/ucinetsoftware/ - WebGraph
http://webgraph.di.unimi.it/
References
- BRANDES, U. & FLEISCHER, D. 2005. Centrality measures based on current flow. In Proceedings of the 22nd International Symposium on Theoretical Aspects of Computer Science (STACS’05), Lecture Notes in Computer Science (LNCS), Springer-Verlag, Vol. 3404, pp. 533–533, 2005.
- CARTER T. BUTTS (2014). sna: Tools for Social Network Analysis. R package version 2.3-2. http://CRAN.R-project.org/package=sna
- STEPHENSON, K. & ZELEN, M. 1989. Rethinking centrality: Methods and examples. Social Networks, 11, 1-37.