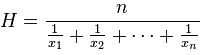Harmonic Centrality
Definition
The denormalized reciprocal of the harmonic mean of all distances (even ∞).
Another extension to networks with disconnected components has been proposed by Opsahl (2010) and later studied by Boldi and Vigna (2014) in general directed graphs: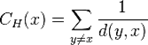
The formula above, with the convention, defines harmonic centrality. It is a natural modification of Bavelas's definition of closeness following the general principle proposed by Marchiori and Latora (2000) that in networks with infinite distances the harmonic mean behaves better than the arithmetic mean. Indeed, Bavelas's closeness can be described as the denormalized reciprocal of the arithmetic mean of distances, whereas harmonic centrality is the denormalized reciprocal of the harmonic mean of distances.
The harmonic mean H of the positive real numbers x1, x2, ..., xn > 0 is defined to be:
See Information Centrality
Putman, K.L., Boekhout, H.D. and Takes, F.W., 2019, August. Fast incremental computation of harmonic closeness centrality in directed weighted networks. In 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM) (pp. 1018-1025). IEEE.
From BOLDI 2014
Yannick Rochat, in a talk at Application of Social Network Analysys (ASNA 2009) observed that in an undirected graph with several disconnected components, the inverse of the harmonic mean of distances offers a better notion of centrality than closeness, because it weights less those elements that belong to smaller components. Tore Opsahl made the same observation in a March 2010 blog posting. Raj Kumar Pan and Jari Saram¨aki deviated from the classical definition of closeness in [Pan and Saram¨aki 11], using, in practice, harmonic centrality, with the motivation of better handling disconnected nodes (albeit with no reference to the harmonic mean). Edith Cohen and Haim Kaplan defined in [Cohen and Kaplan 07] the notion of a spatially decaying aggregate, of which harmonic centrality is a particular instance.
Another extension to networks with disconnected components has been proposed by Opsahl (2010) and later studied by Boldi and Vigna (2014) in general directed graphs:
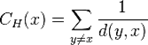
The harmonic mean H of the positive real numbers x1, x2, ..., xn > 0 is defined to be:
See Information Centrality
Putman, K.L., Boekhout, H.D. and Takes, F.W., 2019, August. Fast incremental computation of harmonic closeness centrality in directed weighted networks. In 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM) (pp. 1018-1025). IEEE.
From BOLDI 2014
Yannick Rochat, in a talk at Application of Social Network Analysys (ASNA 2009) observed that in an undirected graph with several disconnected components, the inverse of the harmonic mean of distances offers a better notion of centrality than closeness, because it weights less those elements that belong to smaller components. Tore Opsahl made the same observation in a March 2010 blog posting. Raj Kumar Pan and Jari Saram¨aki deviated from the classical definition of closeness in [Pan and Saram¨aki 11], using, in practice, harmonic centrality, with the motivation of better handling disconnected nodes (albeit with no reference to the harmonic mean). Edith Cohen and Haim Kaplan defined in [Cohen and Kaplan 07] the notion of a spatially decaying aggregate, of which harmonic centrality is a particular instance.
Software
References
- BOLDI, P. & VIGNA, S. 2014. Axioms for centrality. Internet Mathematics, 00-00.
- MARCHIORI, M. & LATORA, V. 2000. Harmony in the small-world. Physica A: Statistical Mechanics and its Applications, 285, 539-546.
- OPSAHL, T., AGNEESSENS, F. & SKVORETZ, J. 2010. Node centrality in weighted networks: Generalizing degree and shortest paths. Social Networks, 32, 245-251.
- OPSAHL, T. 2010. Closeness centrality in networks with disconnected components (http://toreopsahl.com/2010/03/20/closeness-centrality-in-networks-with-disconnected-components/)
Comments
See Holme & Ghoshal, Phys. Rev. Lett. 96, 098701 (2006), Eq. (1) for an earlier reference. (But I don't think it is such a great measure. It is an arbitrary combination of two aspects of networks—the component size distribution and the distances within the components—that rather should be kept separate.) |
|
| Add Replay | written March 24, 2018, 12:14 pm by Petter Holme |