Weighted LeaderRank
Definition
Weighted LeaderRank is a variant to LeaderRank via assigning degree-dependent weights onto links
associated with the ground node.
If network is described by an (N+1)-dimensional weighted adjacency matrix W, so: (i) if aij = 0, then wij = 0; (ii) for any normal node i and the ground node g, wgi = (kini) and wig = 1, where is a free parameter; (iii) for all other cases, wij = 1. After determining the weight of every link, the dynamics follows a biased random walk, namely the score from node j to node i is proportional to the weight wji: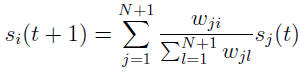 Same to LeaderRank, use final scores in the steady state to quantify nodes’ influences.
Same to LeaderRank, use final scores in the steady state to quantify nodes’ influences.
See also LeaderRank
If network is described by an (N+1)-dimensional weighted adjacency matrix W, so: (i) if aij = 0, then wij = 0; (ii) for any normal node i and the ground node g, wgi = (kini) and wig = 1, where is a free parameter; (iii) for all other cases, wij = 1. After determining the weight of every link, the dynamics follows a biased random walk, namely the score from node j to node i is proportional to the weight wji:
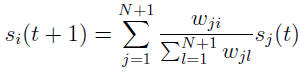
See also LeaderRank
Software
References
- LI, Q., ZHOU, T., LÜ, L. & CHEN, D. 2014. Identifying influential spreaders by weighted LeaderRank. Physica A: Statistical Mechanics and its Applications, 404, 47-55.
DOI: 10.1016/j.physa.2014.02.041

