Subgraph Centrality
Definition
Accounts for the participation of a node in all sub graphs of the network.
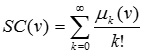 the number of closed walks of length k starting and ending node v in the network is given by the local spectral moments μk(v).
the number of closed walks of length k starting and ending node v in the network is given by the local spectral moments μk(v).
The subgraph centrality is just the diagonal entry of the exponential of the adjacency matrix. Notice that this is not the matrix in which you rise every entry to the exponential. In Matlab there is a function that compute this. For A being the adjacency matrix the function is expm(A) and the subgraph centrality of the nodes is diag(expm(A)).
According to eigenvectors and eigenvalues, if the adjacency matrix is symmetric. Let phi_j(p) be the pth entry of the jth eigenvactor associated with eigenvalue lambda_j of the matrix A. The subgraph centrality is then:
SC(p) = SUM (phi_j(p)^2*exp(lambda_j)
where SUM is the sum over j to n (the number of nodes in the network).
(with thanks to Ernesto Estrada)
Subgraph centrality (SC) of a node is a weighted sum of the numbers of all closed walks of different lengths in the network starting and ending at the node. These closed walks are related to partial subgraphs of a network, e.g., a closed walk with four nodes can ‘‘go through’’ different subgraphs on four nodes, such as along the same edge AB twice (as described above: from node A to node B along edge AB, then back to A along the same edge and then again from A to B and back to A along the same edge), or along a 4-node cycle ABCD that includes edge AB (along the ‘‘square’’ from node A to node B to node C to node D and back to A; this is regardless of whether edges CA and DB that ‘‘go along the diagonal of the square’’ exist) etc. The above mentioned sum is weighted so that the contribution of the closed walks decreases as the length of the walks increases, i.e., shorter walks (smaller subgraphs) have higher weight [MILENKOVIĆ, T., 2011].
Estrada index
Let G=(V,E) be a simple undirected graph with n nodes and let λ1≤λ2≤⋯λn be a non-increasing ordering of the eigenvalues of its adjacency matrix A. The Estrada index is: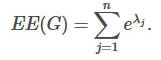 [A HAGBERG, D. S., 2008, ESTRADA, E. 2000]
[A HAGBERG, D. S., 2008, ESTRADA, E. 2000]
Communicability centrality, also called subgraph centrality, of a node n is the sum of closed walks of all lengths starting and ending at node n.
[A HAGBERG, 2008]
See also:
Horton, E., Kloster, K. and Sullivan, B.D., 2019. Subgraph centrality and walk-regularity. Linear Algebra and its Applications, 570, pp.225-244.
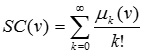
The subgraph centrality is just the diagonal entry of the exponential of the adjacency matrix. Notice that this is not the matrix in which you rise every entry to the exponential. In Matlab there is a function that compute this. For A being the adjacency matrix the function is expm(A) and the subgraph centrality of the nodes is diag(expm(A)).
According to eigenvectors and eigenvalues, if the adjacency matrix is symmetric. Let phi_j(p) be the pth entry of the jth eigenvactor associated with eigenvalue lambda_j of the matrix A. The subgraph centrality is then:
SC(p) = SUM (phi_j(p)^2*exp(lambda_j)
Subgraph centrality (SC) of a node is a weighted sum of the numbers of all closed walks of different lengths in the network starting and ending at the node. These closed walks are related to partial subgraphs of a network, e.g., a closed walk with four nodes can ‘‘go through’’ different subgraphs on four nodes, such as along the same edge AB twice (as described above: from node A to node B along edge AB, then back to A along the same edge and then again from A to B and back to A along the same edge), or along a 4-node cycle ABCD that includes edge AB (along the ‘‘square’’ from node A to node B to node C to node D and back to A; this is regardless of whether edges CA and DB that ‘‘go along the diagonal of the square’’ exist) etc. The above mentioned sum is weighted so that the contribution of the closed walks decreases as the length of the walks increases, i.e., shorter walks (smaller subgraphs) have higher weight [MILENKOVIĆ, T., 2011].
Estrada index
Let G=(V,E) be a simple undirected graph with n nodes and let λ1≤λ2≤⋯λn be a non-increasing ordering of the eigenvalues of its adjacency matrix A. The Estrada index is:
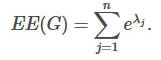
Communicability centrality, also called subgraph centrality, of a node n is the sum of closed walks of all lengths starting and ending at node n.
[A HAGBERG, 2008]
See also:
Horton, E., Kloster, K. and Sullivan, B.D., 2019. Subgraph centrality and walk-regularity. Linear Algebra and its Applications, 570, pp.225-244.
Requirements
Require undirected and loop free network.
Software
References
- A HAGBERG, D. S., P SWART. Exploring Network Structure, Dynamics, and Function using NetworkX. In: G VAROQUAUX, T. V., J MILLMAN, ed. Proceedings of the 7th Python in Science conference (SciPy 2008), 2008. 11-15.
- CSARDI, G. & NEPUSZ, T. 2006. The igraph software package for complex network research. InterJournal, Complex Systems, 1695. [http://igraph.org]
- ESTRADA, E. 2000. Characterization of 3D molecular structure. Chemical Physics Letters, 319, 713-718.
- ESTRADA, E. & RODRIGUEZ-VELAZQUEZ, J. A. 2005. Subgraph centrality in complex networks. Physical Review E, 71, 056103.
- MILENKOVIĆ, T., MEMIŠEVIĆ, V., BONATO, A. & PRŽULJ, N. 2011. Dominating Biological Networks. PLoS ONE, 6, e23016.