Stress Centrality
Definition
The simple accumulation of a number of shortest paths between all node pairs:
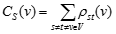 where ρst(v) is the number of shortest paths passing through node v.
where ρst(v) is the number of shortest paths passing through node v.
A node has a high stress if it is traversed by a high number of shortest paths. This parameter is defined only for networks without multiple edges.
The same definition can be applied for edges: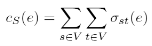 where σst(e) denotes the number of shortest paths containing edge e.
where σst(e) denotes the number of shortest paths containing edge e.
In both cases stress centrality measures the amount of communication that passes an element in an all-to-all scenario. More precisely, it is not only an all-to-all scenario but every vertex sends as many goods or information units to every other vertex as there are shortest paths between them and stress centrality measures the according stress [BRANDES, U. 2005].
The stress is a node centrality index. Stress is calculated by measuring the number of shortest paths passing through a node. To calculate the stress of a node v, all shortest paths in a graph G are calculated and then the number of shortest paths passing through v is counted. A stressed node is a node traversed by a high number of shortest paths. Notably, and importantly, a high stress values does not automatically implies that the node v is critical to maintain the connection between nodes whose paths are passing through it. Indeed, it is possible that two nodes are connected by means of other shortest paths not passing through the node v. Also here, high and low values are more meaningful when compared to the average stress value of the graph G calculated by averaging the stress values of all nodes in the graph.
In biological terms
The stress of a node in a biological network, for instance a protein-signaling network, can indicate the relevance of a protein as functionally capable of holding together communicating nodes. The higher the value the higher the relevance of the protein in connecting regulatory molecules. Due to the nature of this centrality, it is possible that the stress simply indicates a molecule heavily involved in cellular processes but not relevant to maintain the communication between other proteins. [SCARDONI, G.,]
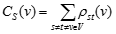
A node has a high stress if it is traversed by a high number of shortest paths. This parameter is defined only for networks without multiple edges.
The same definition can be applied for edges:
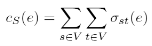
In both cases stress centrality measures the amount of communication that passes an element in an all-to-all scenario. More precisely, it is not only an all-to-all scenario but every vertex sends as many goods or information units to every other vertex as there are shortest paths between them and stress centrality measures the according stress [BRANDES, U. 2005].
The stress is a node centrality index. Stress is calculated by measuring the number of shortest paths passing through a node. To calculate the stress of a node v, all shortest paths in a graph G are calculated and then the number of shortest paths passing through v is counted. A stressed node is a node traversed by a high number of shortest paths. Notably, and importantly, a high stress values does not automatically implies that the node v is critical to maintain the connection between nodes whose paths are passing through it. Indeed, it is possible that two nodes are connected by means of other shortest paths not passing through the node v. Also here, high and low values are more meaningful when compared to the average stress value of the graph G calculated by averaging the stress values of all nodes in the graph.
In biological terms
The stress of a node in a biological network, for instance a protein-signaling network, can indicate the relevance of a protein as functionally capable of holding together communicating nodes. The higher the value the higher the relevance of the protein in connecting regulatory molecules. Due to the nature of this centrality, it is possible that the stress simply indicates a molecule heavily involved in cellular processes but not relevant to maintain the communication between other proteins. [SCARDONI, G.,]
Requirements
Require connected and loop free network.
Software
- CentiBiN
http://centibin.ipk-gatersleben.de/ - CentiLib
http://centilib.ipk-gatersleben.de/ - CentiScaPe
http://www.cbmc.it/~scardonig/centiscape/centiscape.php - Interference
http://www.cbmc.it/~scardonig/interference/Interference.php - neo4j
http://neo4j.com/ - NetworkAnalyzer
http://med.bioinf.mpi-inf.mpg.de/networkanalyzer/ - sna
http://CRAN.R-project.org/package=sna - SocNetV
http://socnetv.sourceforge.net/ - Visone
http://visone.info/
References
- BRANDES, U. & ERLEBACH, T. 2005. Network Analysis: Methodological Foundations, U.S. Government Printing Office.
- CARTER T. BUTTS (2014). sna: Tools for Social Network Analysis. R package version 2.3-2. http://CRAN.R-project.org/package=sna
- SCARDONI, G., LAUDANNA, C., TOSADORI, G., FABBRI, F. & FAIZAAN, M. CentiScaPe: Network centralities for Cytoscape. http://www.cbmc.it/~scardonig/centiscape/CentiScaPefiles/CentralitiesTutorial.pdf
- SCARDONI, G., PETTERLINI, M. & LAUDANNA, C. 2009. Analyzing biological network parameters with CentiScaPe. Bioinformatics, 25, 2857-2859.
DOI: 10.1093/bioinformatics/btp517


- SHIMBEL, A. 1953. Structural parameters of communication networks. The bulletin of mathematical biophysics, 15, 501-507.