Shortest-Paths Betweenness Centrality
Definition
Ratio of the number of shortest paths passing through a node v out of all shortest paths between all node pairs in a network:
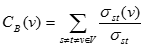 σst is the number of shortest paths between node s and t and σst(v) is the number of shortest paths passing on a node v out σst
σst is the number of shortest paths between node s and t and σst(v) is the number of shortest paths passing on a node v out σst
The S.-P. Betweenness is a node centrality index. It is similar to the stress but provides a more elaborated and informative centrality index. It is calculated considering couples of nodes (v1, v2) and counting the number of shortest paths linking v1 and v2 and passing through a node n. Then, the value is related to the total number of shortest paths linking v1 and v2. Thus, a node can be traversed by only one path linking v1 and v2, but if this path is the only connecting v1 and v2 the node n will score a higher betweenness value (in the stress computation would have had a low score). Thus, a high S.-P. Betweenness score means that the node, for certain paths, is crucial to maintain node connections. Notably, to know the number of paths for which the node is critical it is necessary to look at the stress. Thus, stress and S.-P. Betweenness can be used to gain complementary information. Further information could be gained by referring the S.-P. Betweenness to node couples, thus quantifying the importance of a node for two connected nodes. Also here, high and low values are more meaningful when compared to the average S.-P. Betweenness value of the graph G calculated by averaging the S.-P. Betweenness values of all nodes in the graph.
The S.-P. Betweenness of a node in a biological network, for instance a protein-signaling network, can indicate the relevance of a protein as functionally capable of holding together communicating proteins. The higher the value the higher the relevance of the protein as organizing regulatory molecule. The S.-P. Betweenness of a protein effectively indicates the capability of a protein to bring in communication distant proteins. In signaling modules, proteins with high S.-P. Betweenness are likely crucial to maintain functionally and coherence of signaling mechanisms. [SCARDONI, G.,]
See:
ABRA - Approximating Betweenness Centrality
Approximating Betweenness Centrality
K-step Betweenness Centrality
Edge Betweenness centrality
Bröhl, T. and Lehnertz, K., 2019. Centrality-based identification of important edges in complex networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 29(3), p.033115.
Incremental Betweenness Centrality
Jamour, F., Skiadopoulos, S. and Kalnis, P., 2017. Parallel Algorithm for Incremental Betweenness Centrality on Large Graphs. IEEE Transactions on Parallel and Distributed Systems.
Akgün, M.K. and Tural, M.K., 2020. k-step betweenness centrality. Computational and Mathematical Organization Theory, 26(1), pp.55-87.
Bromberger, S., Klymko, C., Henderson, K., Pearce, R. and Sanders, G., Improving Estimation of Betweenness Centrality for Scale-Free Graphs.
Brandes, U., 2001. A faster algorithm for betweenness centrality. Journal of mathematical sociology, 25(2), pp.163-177.
Matta, J., 2017, November. A Comparison of Approaches to Computing Betweenness Centrality for Large Graphs. In International Workshop on Complex Networks and their Applications (pp. 3-13). Springer, Cham.
Bentert, M., Dittmann, A., Kellerhals, L., Nichterlein, A. and Niedermeier, R., 2018. Towards Improving Brandes' Algorithm for Betweenness Centrality. arXiv preprint arXiv:1802.06701.
Maurya, S.K., Liu, X. and Murata, T., 2019, November. Fast Approximations of Betweenness Centrality with Graph Neural Networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management (pp. 2149-2152).
Behera, R.K., Naik, D., Ramesh, D. and Rath, S.K., 2020. MR-IBC: MapReduce-based incremental betweenness centrality in large-scale complex networks. Social Network Analysis and Mining, 10, pp.1-13.
Shukla, K., Regunta, S.C., Tondomker, S.H. and Kothapalli, K., 2020, June. Efficient parallel algorithms for betweenness-and closeness-centrality in dynamic graphs. In Proceedings of the 34th ACM International Conference on Supercomputing (pp. 1-12).
Wandelt, S., Shi, X. and Sun, X., 2020. Approximation of Interactive Betweenness Centrality in Large Complex Networks. Complexity, 2020.
Zaoli, S., Mazzarisi, P. and Lillo, F., 2020. Betweenness centrality for temporal multiplexes. arXiv preprint arXiv:2002.00661.
Nakajima, K., Iwasaki, K., Matsumura, T. and Shudo, K., 2018, December. Estimating top-k betweenness centrality nodes in online social networks. In 2018 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Ubiquitous Computing & Communications, Big Data & Cloud Computing, Social Computing & Networking, Sustainable Computing & Communications (ISPA/IUCC/BDCloud/SocialCom/SustainCom) (pp. 1128-1135). IEEE.
Hanzelka, J., Běloch, M., Martinovič, J. and Slaninová, K., 2019. Vertex importance extension of betweenness centrality algorithm. In Data Management, Analytics and Innovation (pp. 61-72). Springer, Singapore.
Kumari, P. and Singh, A., 2019. Approximation and updation of betweenness centrality in dynamic complex networks. In Computational Intelligence: Theories, Applications and Future Directions-Volume I (pp. 25-37). Springer, Singapore.
Xue, H., Li, T. and Luo, X., 2019, May. Identification of Key Nodes by Algorithm of Betweenness Centrality Based on Traversal of Spark Graph. In 2019 International Conference on Computer, Network, Communication and Information Systems (CNCI 2019) (pp. 299-305). Atlantis Press.
Chehreghani, M.H., Bifet, A. and Abdessalem, T., 2018, December. DyBED: An efficient algorithm for updating betweenness centrality in directed dynamic graphs. In 2018 IEEE International Conference on Big Data (Big Data) (pp. 2114-2123). IEEE.
Hoang, L., Pontecorvi, M., Dathathri, R., Gill, G., You, B., Pingali, K. and Ramachandran, V., 2019, February. A round-efficient distributed betweenness centrality algorithm. In Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming (pp. 272-286).
Unnithan, S.K.R. and Balakrishnan, K., 2019. Betweenness centrality in convex amalgamation of graphs. Journal of Algebra Combinatorics Discrete Structures and Applications, 6(1), pp.21-38.
Ji, S. and Yan, Z., 2016. Refining approximating betweenness centrality based on samplings. arXiv preprint arXiv:1608.04472.
Artiles, O. and Saeed, F., 2021, August. TurboBC: A Memory Efficient and Scalable GPU Based Betweenness Centrality Algorithm in the Language of Linear Algebra. In 50th International Conference on Parallel Processing Workshop (pp. 1-10).
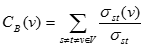
The S.-P. Betweenness is a node centrality index. It is similar to the stress but provides a more elaborated and informative centrality index. It is calculated considering couples of nodes (v1, v2) and counting the number of shortest paths linking v1 and v2 and passing through a node n. Then, the value is related to the total number of shortest paths linking v1 and v2. Thus, a node can be traversed by only one path linking v1 and v2, but if this path is the only connecting v1 and v2 the node n will score a higher betweenness value (in the stress computation would have had a low score). Thus, a high S.-P. Betweenness score means that the node, for certain paths, is crucial to maintain node connections. Notably, to know the number of paths for which the node is critical it is necessary to look at the stress. Thus, stress and S.-P. Betweenness can be used to gain complementary information. Further information could be gained by referring the S.-P. Betweenness to node couples, thus quantifying the importance of a node for two connected nodes. Also here, high and low values are more meaningful when compared to the average S.-P. Betweenness value of the graph G calculated by averaging the S.-P. Betweenness values of all nodes in the graph.
The S.-P. Betweenness of a node in a biological network, for instance a protein-signaling network, can indicate the relevance of a protein as functionally capable of holding together communicating proteins. The higher the value the higher the relevance of the protein as organizing regulatory molecule. The S.-P. Betweenness of a protein effectively indicates the capability of a protein to bring in communication distant proteins. In signaling modules, proteins with high S.-P. Betweenness are likely crucial to maintain functionally and coherence of signaling mechanisms. [SCARDONI, G.,]
See:
ABRA - Approximating Betweenness Centrality
Approximating Betweenness Centrality
K-step Betweenness Centrality
Edge Betweenness centrality
Bröhl, T. and Lehnertz, K., 2019. Centrality-based identification of important edges in complex networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 29(3), p.033115.
Incremental Betweenness Centrality
Jamour, F., Skiadopoulos, S. and Kalnis, P., 2017. Parallel Algorithm for Incremental Betweenness Centrality on Large Graphs. IEEE Transactions on Parallel and Distributed Systems.
Akgün, M.K. and Tural, M.K., 2020. k-step betweenness centrality. Computational and Mathematical Organization Theory, 26(1), pp.55-87.
Bromberger, S., Klymko, C., Henderson, K., Pearce, R. and Sanders, G., Improving Estimation of Betweenness Centrality for Scale-Free Graphs.
Brandes, U., 2001. A faster algorithm for betweenness centrality. Journal of mathematical sociology, 25(2), pp.163-177.
Matta, J., 2017, November. A Comparison of Approaches to Computing Betweenness Centrality for Large Graphs. In International Workshop on Complex Networks and their Applications (pp. 3-13). Springer, Cham.
Bentert, M., Dittmann, A., Kellerhals, L., Nichterlein, A. and Niedermeier, R., 2018. Towards Improving Brandes' Algorithm for Betweenness Centrality. arXiv preprint arXiv:1802.06701.
Maurya, S.K., Liu, X. and Murata, T., 2019, November. Fast Approximations of Betweenness Centrality with Graph Neural Networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management (pp. 2149-2152).
Behera, R.K., Naik, D., Ramesh, D. and Rath, S.K., 2020. MR-IBC: MapReduce-based incremental betweenness centrality in large-scale complex networks. Social Network Analysis and Mining, 10, pp.1-13.
Shukla, K., Regunta, S.C., Tondomker, S.H. and Kothapalli, K., 2020, June. Efficient parallel algorithms for betweenness-and closeness-centrality in dynamic graphs. In Proceedings of the 34th ACM International Conference on Supercomputing (pp. 1-12).
Wandelt, S., Shi, X. and Sun, X., 2020. Approximation of Interactive Betweenness Centrality in Large Complex Networks. Complexity, 2020.
Zaoli, S., Mazzarisi, P. and Lillo, F., 2020. Betweenness centrality for temporal multiplexes. arXiv preprint arXiv:2002.00661.
Nakajima, K., Iwasaki, K., Matsumura, T. and Shudo, K., 2018, December. Estimating top-k betweenness centrality nodes in online social networks. In 2018 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Ubiquitous Computing & Communications, Big Data & Cloud Computing, Social Computing & Networking, Sustainable Computing & Communications (ISPA/IUCC/BDCloud/SocialCom/SustainCom) (pp. 1128-1135). IEEE.
Hanzelka, J., Běloch, M., Martinovič, J. and Slaninová, K., 2019. Vertex importance extension of betweenness centrality algorithm. In Data Management, Analytics and Innovation (pp. 61-72). Springer, Singapore.
Kumari, P. and Singh, A., 2019. Approximation and updation of betweenness centrality in dynamic complex networks. In Computational Intelligence: Theories, Applications and Future Directions-Volume I (pp. 25-37). Springer, Singapore.
Xue, H., Li, T. and Luo, X., 2019, May. Identification of Key Nodes by Algorithm of Betweenness Centrality Based on Traversal of Spark Graph. In 2019 International Conference on Computer, Network, Communication and Information Systems (CNCI 2019) (pp. 299-305). Atlantis Press.
Chehreghani, M.H., Bifet, A. and Abdessalem, T., 2018, December. DyBED: An efficient algorithm for updating betweenness centrality in directed dynamic graphs. In 2018 IEEE International Conference on Big Data (Big Data) (pp. 2114-2123). IEEE.
Hoang, L., Pontecorvi, M., Dathathri, R., Gill, G., You, B., Pingali, K. and Ramachandran, V., 2019, February. A round-efficient distributed betweenness centrality algorithm. In Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming (pp. 272-286).
Unnithan, S.K.R. and Balakrishnan, K., 2019. Betweenness centrality in convex amalgamation of graphs. Journal of Algebra Combinatorics Discrete Structures and Applications, 6(1), pp.21-38.
Ji, S. and Yan, Z., 2016. Refining approximating betweenness centrality based on samplings. arXiv preprint arXiv:1608.04472.
Artiles, O. and Saeed, F., 2021, August. TurboBC: A Memory Efficient and Scalable GPU Based Betweenness Centrality Algorithm in the Language of Linear Algebra. In 50th International Conference on Parallel Processing Workshop (pp. 1-10).
Software
- AllegroGraph
http://franz.com/agraph/allegrograph/ - The Brain Connectivity Toolbox (BCT)
http://www.brain-connectivity-toolbox.net/ - CentiBiN
http://centibin.ipk-gatersleben.de/ - CentiLib
http://centilib.ipk-gatersleben.de/ - CentiScaPe
http://www.cbmc.it/~scardonig/centiscape/centiscape.php - CytoNCA
http://apps.cytoscape.org/apps/cytonca - EgoNet
http://escoladeredes.net/profiles/blogs/egonet-1 - Functional Genomics Assistant (FUGA)
http://code.google.com/p/fuga - GraphStream
http://graphstream-project.org/ - graph-tool
http://graph-tool.skewed.de/ - GTNA
https://www.p2p.tu-darmstadt.de/research/gtna/ - igraph
http://igraph.org - Interference
http://www.cbmc.it/~scardonig/interference/Interference.php - JGraphT-sna
https://bitbucket.org/sorend/jgrapht-sna - JUNG
http://jung.sourceforge.net - MultiNet
http://www.sfu.ca/personal/archives/richards/Multinet/Pages/multinet.htm - neo4j
http://neo4j.com/ - NetVis Module
http://www.netvis.org/ Module
- NetworkAnalyzer
http://med.bioinf.mpi-inf.mpg.de/networkanalyzer/ - NetworKit
https://networkit.iti.kit.edu/ - NetworkX
https://networkx.github.io/ - NodeXL
http://nodexl.codeplex.com/ - Pajek
http://pajek.imfm.si/ - qgraph
http://sachaepskamp.com/qgraph - RBGL
http://www.bioconductor.org/packages/release/bioc/html/RBGL.html - RINalyzer
http://rinalyzer.de/ - RINspector
http://apps.cytoscape.org/apps/rinspector - SBEToolbox
https://github.com/biocoder/SBEToolbox/releases - Sentinel Visualizer
http://www.fmsasg.com/SocialNetworkAnalysis/ - sna
http://CRAN.R-project.org/package=sna - SocNetV
http://socnetv.sourceforge.net/ - tnet
http://cran.r-project.org/web/packages/tnet/ - UCINET
https://sites.google.com/site/ucinetsoftware/ - Visone
http://visone.info/ - WebGraph
http://webgraph.di.unimi.it/ - Wolfram
http://www.wolfram.com
References
- SCARDONI, G., LAUDANNA, C., TOSADORI, G., FABBRI, F. & FAIZAAN, M. CentiScaPe: Network centralities for Cytoscape. http://www.cbmc.it/~scardonig/centiscape/CentiScaPefiles/CentralitiesTutorial.pdf
- SCARDONI, G., PETTERLINI, M. & LAUDANNA, C. 2009. Analyzing biological network parameters with CentiScaPe. Bioinformatics, 25, 2857-2859.
DOI: 10.1093/bioinformatics/btp517


- FREEMAN, L. C. 1977. A set of measures of centrality based on betweenness. Sociometry, 35-41.
- Chehreghani, M.H., Bifet, A. and Abdessalem, T., 2017. Efficient Exact and Approximate Algorithms for Computing Betweenness Centrality in Directed Graphs. arXiv preprint arXiv:1708.08739.