Principal Component Centrality
Definition
Principal Component Centrality (PCC) of a node in a graph as the
Euclidean distance/l2 norm of a node from the origin in the
P-dimensional eigenspace formed by the P most significant
eigenvectors. For a graph consisting of a single connected
component, the N eigenvalues |λ1|≥|λ2|≥...≥|λN| = 0
correspond to the normalized eigenvectors X1 , X2 , ... ,XN.
The eigenvector/eigenvalue pairs are indexed in order of
descending magnitude of eigenvalues.
Let X denote the N x N matrix of concatenated eigenvectors X = [X1X2 ... XN] and let Λ = [λ1,λ2 ... λN]' be the vector of eigenvalues. Furthermore, if P < N and if matrix X has dimensions N x N , then XNxP will denote the submatrix of X consisting of the first N rows and first P columns. Then PCC can be expressed in matrix form as: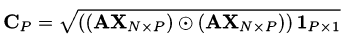 Above equation can also be written in
terms of the eigenvalue and eigenvector matrices Λ and X, of
the adjacency matrix A:
Above equation can also be written in
terms of the eigenvalue and eigenvector matrices Λ and X, of
the adjacency matrix A:
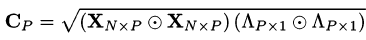
PCC is a measure of node centrality and is based on PCA and the Karhunen Loeve transform (KLT) which takes the view of treating a graphs adjacency matrix as a covariance matrix.
Unlike eigenvector centrality, PCC allows the addition of more features for the computation of node centralities.
Li, J.R., YU, L. and ZHAO, J., 2014. A Node Centrality Evaluation Model for Weighted Social Networks. Journal of University of Electronic Science and Technology of China, 43(3), pp.322-328.
Let X denote the N x N matrix of concatenated eigenvectors X = [X1X2 ... XN] and let Λ = [λ1,λ2 ... λN]' be the vector of eigenvalues. Furthermore, if P < N and if matrix X has dimensions N x N , then XNxP will denote the submatrix of X consisting of the first N rows and first P columns. Then PCC can be expressed in matrix form as:
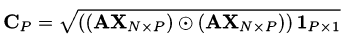
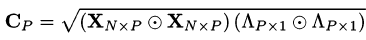
PCC is a measure of node centrality and is based on PCA and the Karhunen Loeve transform (KLT) which takes the view of treating a graphs adjacency matrix as a covariance matrix.
Unlike eigenvector centrality, PCC allows the addition of more features for the computation of node centralities.
Weighted Principal Component Centrality
Li, J.R., YU, L. and ZHAO, J., 2014. A Node Centrality Evaluation Model for Weighted Social Networks. Journal of University of Electronic Science and Technology of China, 43(3), pp.322-328.
Software
References
- ILYAS, M. U. & RADHA, H. A KLT-inspired node centrality for identifying influential neighborhoods in graphs. Information Sciences and Systems (CISS), 2010 44th Annual Conference on, 17-19 March 2010 2010. 1-7.
Comments
Good day, Wonderful work, I have been searching all over the internet on principal component centrality computation and here it is in your website. kindly assist me on how to implement this particalar centrality using either the centiserver or centiserve please, my email address is toomuch086@yahoo.com. I look forward to hearing from you soon. Thank you. Murtala Sheriff. |
|
| Add Replay | written April 27, 2016, 3:00 am by Sheriff Murtala |