Pairwise Disconnectivity Index
Definition
The pairwise disconnectivity defined as index of vertex v, Dis(v), as the fraction of those initially
connected pairs of vertices in a network which become
disconnected if vertex v is removed from the network
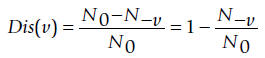 Here, N0 is the total number of ordered pairs of vertices in
a network that are connected by at least one directed path
of any length. It is supposed that N0 > 0, i.e., there exists at
least one edge in the network that links two different vertices.
N-v is the number of ordered pairs that are still connected
after removing vertex v from the network, via
alternative paths through other vertices.
Here, N0 is the total number of ordered pairs of vertices in
a network that are connected by at least one directed path
of any length. It is supposed that N0 > 0, i.e., there exists at
least one edge in the network that links two different vertices.
N-v is the number of ordered pairs that are still connected
after removing vertex v from the network, via
alternative paths through other vertices.
The pairwise disconnectivity index quantifies how crucial an individual element is for sustaining the communication ability between connected pairs of vertices in a network that is displayed as a directed graph.
Mediative Disconnectivity Index
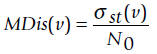 σst(v) expresses the number of ordered
pairs {s,t} ¦ s ≠ t ≠ v and s, t, v ∈ V that are exclusively
linked through vertex v.
σst(v) expresses the number of ordered
pairs {s,t} ¦ s ≠ t ≠ v and s, t, v ∈ V that are exclusively
linked through vertex v.
It immediately detects the fraction of connected ordered pairs of vertices different from v for whose reachability vertex v is necessary.
In a directed network, an ordered pair of vertices (i,j) consists of two distinct nodes i and j. Such a pair is connected if there exists at least one path of any length from vertex i to vertex j. The pair (i,j) differs from the ordered pair (j,i), which is connected if there is a path from vertex j to vertex i. In an undirected network all pairs are unordered, i.e. (i,j) = (j,i).
Let G be a (directed) graph and N the number of connected (ordered) pairs of vertices in G. The PDI of a network entity is defined as:
and always ranges between 0 and 1. The maximum PDI of 1 means that no ordered pair of vertices in G is linked anymore due to the deletion of the entity whereas 0 indicates that all ordered pairs in G are still linked.
Note, that the meaning of N' depends on the chosen network entity. An entity may be
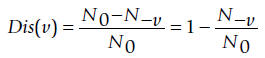
The pairwise disconnectivity index quantifies how crucial an individual element is for sustaining the communication ability between connected pairs of vertices in a network that is displayed as a directed graph.
Mediative Disconnectivity Index
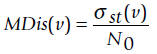
It immediately detects the fraction of connected ordered pairs of vertices different from v for whose reachability vertex v is necessary.
From DiVa site:
The pairwise disconnectivity index (PDI) evaluates the topological significance of a network entity (vertex, edge, groups of vertices/edges) based on its influence on the connectedness of a network. This can be quantified by estimating how the deletion of an entity affects the existing number of connected ordered pairs of vertices in a network. The more of these pairs are being disconnected upon the removal of a network entity the more important it is.In a directed network, an ordered pair of vertices (i,j) consists of two distinct nodes i and j. Such a pair is connected if there exists at least one path of any length from vertex i to vertex j. The pair (i,j) differs from the ordered pair (j,i), which is connected if there is a path from vertex j to vertex i. In an undirected network all pairs are unordered, i.e. (i,j) = (j,i).
Let G be a (directed) graph and N the number of connected (ordered) pairs of vertices in G. The PDI of a network entity is defined as:
PDI(entity) = 1 - N'/N
and always ranges between 0 and 1. The maximum PDI of 1 means that no ordered pair of vertices in G is linked anymore due to the deletion of the entity whereas 0 indicates that all ordered pairs in G are still linked.
Note, that the meaning of N' depends on the chosen network entity. An entity may be
- a single vertex v: N' refers to the number of connected
(ordered) pairs of vertices in G without v and its edges.
- a group of vertices, e.g. {a,b,c}: N' is the number of connected (ordered) pairs of vertices in G without the vertices a,b,c and their edges.
- a single edge e: N' is the number of connected (ordered) pairs of vertices in G without e.
- a group of edges, e.g. {a -> b,c -> a}: N' is the number of connected (ordered) pairs of vertices in G without the edges a -> b and c -> a.
- a topological pattern or a pattern instance: in a directed graph G, a pattern is the joint feature of every n connected vertices and describes the way how n vertices are connected with each other. A pattern always comprehends all existing edges between n vertices. None of the n vertices is isolated from the others, i.e. each of the n vertices must be directly attached to at least another one. If a pattern is over-represented in G it is usually called a motif.
Requirements
Require directed network.
Software
- DiVa
DiVa - Disconnectivity Valuation tool - DiVa online
DiVa online
References
- POTAPOV, A. P., GOEMANN, B. & WINGENDER, E. 2008. The pairwise disconnectivity index as a new metric for the topological analysis of regulatory networks. BMC bioinformatics, 9, 227.