Laplacian Centrality
Definition
If G is a graph of n vertices, then the Laplacian centrality with respect to v is:
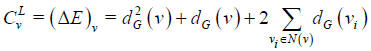 where N(v) is the set of neighbors of v in G and dG(vi) is the degree of vi in G.
where N(v) is the set of neighbors of v in G and dG(vi) is the degree of vi in G.
Laplacian centrality is a simple centrality measure that can be calculated in linear time. It is defined as the drop in the Laplacian energy (i.e. sum of squares of the eigenvalues in the Laplacian matrix) of the graph when the vertex is removed.
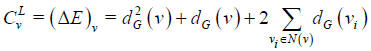
Laplacian centrality is a simple centrality measure that can be calculated in linear time. It is defined as the drop in the Laplacian energy (i.e. sum of squares of the eigenvalues in the Laplacian matrix) of the graph when the vertex is removed.
See:
Incremental Laplacian Centrality
Dynamic laplace
Cordeiro, M., Sarmento, R.P., Brazdil, P. and Gama, J., 2018. Dynamic laplace: efficient centrality measure for weighted or unweighted evolving networks. arXiv preprint arXiv:1808.02960.
Boley, D., Buendia, A. and Golnari, G., 2018. Random Walk Laplacian and Network Centrality Measures. arXiv preprint arXiv:1808.02912.
Software
References
- QI, X., DUVAL, R. D., CHRISTENSEN, K., FULLER, E., SPAHIU, A., WU, Q., WU, Y., TANG, W. & ZHANG, C. 2013. Terrorist networks, network energy and node removal: a new measure of centrality based on Laplacian energy. Social Networking, 2, 19.
- QI, X., FULLER, E., WU, Q., WU, Y. & ZHANG, C.-Q. 2012. Laplacian centrality: A new centrality measure for weighted networks. Information Sciences, 194, 240-253.
- Baruah, D. and Bharali, A., A Comparative Study of Vertex Deleted Centrality Measures.
Comments
Hi, Thank you for this great resource pool! I have a question regarding the laplacian centrality measure. In the R package centiserve it seems to compute laplacian centrality only for unweighted graphs. Do you perhaps know how I can compute laplacian centrlaity and the total graph energy for directed and weighted graphs? Yingjie |
|
| Add Replay | written October 23, 2018, 2:11 pm by Yingjie |
Hi. I have the same question about laplacian centrality with Yingjie. In the package manual, the laplacian function does not seem to have an option for weights. But, QI, X, et al (2012) extended it for weighted networks as referenced above. So. does the laplacian function can measure directed and weighted networks? Thank you in advance. Joon |
|
| Add Replay | written September 19, 2019, 6:14 am by Joon Jun |