Knotty Centrality
Definition
A network measure called knotty-centrality is defined that quantifies the extent to which a given subset of a graph’s nodes
constitutes a densely intra-connected topologically central connective core. Using this measure, the knotty centre of a
network is defined as a sub-graph with maximal knotty-centrality.
Consider a directed graph G with N nodes. The knotty-centrality of a (non-empty, non-singleton) subset S of the nodes in G is given by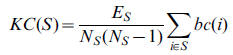 where Es is the number of edges between nodes in S, and Ns is the
number of nodes in S. bc(i) is the betweenness centrality of node i
normalised with respect to the whole graph, such that
where Es is the number of edges between nodes in S, and Ns is the
number of nodes in S. bc(i) is the betweenness centrality of node i
normalised with respect to the whole graph, such that
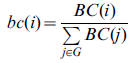 where BC(i) is the (directed) betweenness centrality of node i. Knotty-centrality ranges from 0 to 1. It is 0
if none of the nodes in S is adjacent (Es=0): It is 1 if S is a clique
and
where BC(i) is the (directed) betweenness centrality of node i. Knotty-centrality ranges from 0 to 1. It is 0
if none of the nodes in S is adjacent (Es=0): It is 1 if S is a clique
and 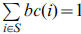 . If G is a clique then
. If G is a clique then
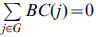 and KC(S) is
undefined. The measure can be applied to either weighted or
unweighted graphs by substituting weighted or unweighted
variants of betweenness centrality into equation.
and KC(S) is
undefined. The measure can be applied to either weighted or
unweighted graphs by substituting weighted or unweighted
variants of betweenness centrality into equation.
Consider a directed graph G with N nodes. The knotty-centrality of a (non-empty, non-singleton) subset S of the nodes in G is given by
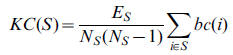
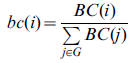
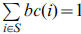 . If G is a clique then
. If G is a clique then
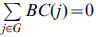 and KC(S) is
undefined. The measure can be applied to either weighted or
unweighted graphs by substituting weighted or unweighted
variants of betweenness centrality into equation.
and KC(S) is
undefined. The measure can be applied to either weighted or
unweighted graphs by substituting weighted or unweighted
variants of betweenness centrality into equation.
Software
References
- SHANAHAN, M. & WILDIE, M. 2012. Knotty-centrality: finding the connective core of a complex network. PloS one, 7, e36579.