There are no comment yet.
Graphlet Degree Centrality
Definition
Graphlet Degree Centrality (GDC) captures the density and topological complexity of up to 4-deep network neighborhood around a node.
Graphlets are small, connected, induced, non-isomorphic subgraphs of a large network. More precisely, coordinates of a GDV count how many times a node is touched by a particular symmetry group (automorphism orbit) within a graphlet. Clearly, the degree of a node is the first coordinate in GDV, since an edge is the only 2-node graphlet. There is a total of 73 orbits in all 2–5-node graphlets. Thus, the GDV of a node, describing its up to 4-deep neighborhood (i.e., 2–5-node graphlets around it), has 73 coordinates.
GDC measures the density of the node’s extended network neighborhood. Hence, nodes that reside in dense extended network neighborhoods will have higher GDCs than nodes that reside in sparse extended network neighborhoods. In particular, we define GDC as follows. For a node v, we denote by vi the ith coordinate of its GDV, i.e., vi is the number of times node v touches an orbit i. Then, GDC of node v is computed as follows: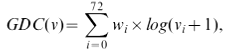
where wi is the weight of orbit i that accounts for dependencies between orbits, e.g., counts of orbit 3, a triangle, will affect counts of all orbits that contain a triangle. Hence, for each orbit, we count how many orbits affect it and assign a higher weight wi (wi∈[0,1]) to the orbits that are not affected by many other orbits. We use log in the formula because the coordinates i and j of the GDV of node v can differ by several orders of magnitude and we do not want the GDC to be entirely dominated by orbits with very large values. We add 1 to vi in the formula to prevent the logarithm function to go to infinity for an orbit count of 0. Finally, we scale the value of the GDC(v) to (0,1] by dividing it with the maximum GDC(u) over all nodes u in the network.
[MILENKOVIĆ, T. 2011]
Graphlets are small, connected, induced, non-isomorphic subgraphs of a large network. More precisely, coordinates of a GDV count how many times a node is touched by a particular symmetry group (automorphism orbit) within a graphlet. Clearly, the degree of a node is the first coordinate in GDV, since an edge is the only 2-node graphlet. There is a total of 73 orbits in all 2–5-node graphlets. Thus, the GDV of a node, describing its up to 4-deep neighborhood (i.e., 2–5-node graphlets around it), has 73 coordinates.
GDC measures the density of the node’s extended network neighborhood. Hence, nodes that reside in dense extended network neighborhoods will have higher GDCs than nodes that reside in sparse extended network neighborhoods. In particular, we define GDC as follows. For a node v, we denote by vi the ith coordinate of its GDV, i.e., vi is the number of times node v touches an orbit i. Then, GDC of node v is computed as follows:
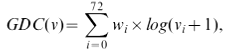
Software
- GraphCrunch
http://bio-nets.doc.ic.ac.uk/graphcrunch2/
References
- MILENKOVIĆ, T., MEMIŠEVIĆ, V., BONATO, A. & PRŽULJ, N. 2011. Dominating biological networks. PloS one, 6, e23016.