Fuzzy Closeness Centrality
Definition
Closeness centrality measures how close a node is to all
other nodes. This definition closely relates to fuzzy concepts:
1) the concept of close is a fuzzy linguistic variable, and the
concept of all other is a fuzzy universal quantifier.
A generalized fuzzy centrality measure is defined as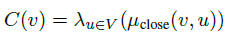 First, there is a path closeness function for a given node v:μclose : (v, u) → [0; 1] which maps possible information flow
between a node-pair into a value in the unit interval. Secondly,
an aggregation function λ : [0, 1]n → [0, 1], which aggregates
these information flows into a single value. Here λ is chosen
from the set of andness-directed operators.
First, there is a path closeness function for a given node v:μclose : (v, u) → [0; 1] which maps possible information flow
between a node-pair into a value in the unit interval. Secondly,
an aggregation function λ : [0, 1]n → [0, 1], which aggregates
these information flows into a single value. Here λ is chosen
from the set of andness-directed operators.
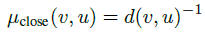 Following, the AIWA operator can be plugged in for λ, to
get the aggregate measure of closeness to all other nodes, as
seen in:
Following, the AIWA operator can be plugged in for λ, to
get the aggregate measure of closeness to all other nodes, as
seen in:
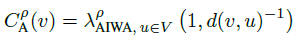 When ρ < 0:5 the measure increases the ranking of nodes
which have many close nodes, and for ρ > 0:5 ranking is
increased for nodes close to all nodes. For ρ = 0:5 the ranking
is equal to that of the classic closeness centrality measure.
When ρ < 0:5 the measure increases the ranking of nodes
which have many close nodes, and for ρ > 0:5 ranking is
increased for nodes close to all nodes. For ρ = 0:5 the ranking
is equal to that of the classic closeness centrality measure.
A generalized fuzzy centrality measure is defined as
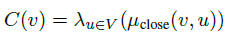
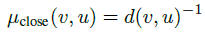
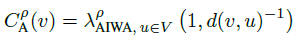
References
- S. A. Davidsen and M. Padmavathamma. A fuzzy closeness-centrality with andness-direction to control degree of closeness. In Proc. 1st Int. Conf. on Networks and Soft Computing, pp. 225-230, 2014.