Flux Centrality
Definition
This centrality developed based on the concept of maximum flow. Considering any two vertices s and t in a network, the maximum flow between the two is defined by the largest flow that is observed for all possible paths connecting the two [AHUJA, R. K., 1993]. In simple terms, out of the many connecting paths we are looking for a set of paths forming the ‘strongest carbon flux’ connecting s and t. Denote this maximum flow between s and t as max_flow (s,t). According shortest-path closeness centrality, which sums the lengths of the shortest-paths from a vertex s to all other vertices t (t∈V, V is the set of all vertices in the network), the maximum-flow closeness defined as:
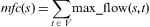 For each vertex the resulting value of the maximum-flow closeness centrality might be interpreted as a ‘metabolic potential’ of the respective metabolite. The higher an mfc value of a metabolite, the more of it is converted into other metabolites throughout the network. It should be noted that a more precise name of the defined centrality is out-maximum-flow closeness, because the flow leaving the vertex of interest is computed and a corresponding in-maximum-flow closeness, computing the flow entering the vertex, might be defined in a similar way.
For each vertex the resulting value of the maximum-flow closeness centrality might be interpreted as a ‘metabolic potential’ of the respective metabolite. The higher an mfc value of a metabolite, the more of it is converted into other metabolites throughout the network. It should be noted that a more precise name of the defined centrality is out-maximum-flow closeness, because the flow leaving the vertex of interest is computed and a corresponding in-maximum-flow closeness, computing the flow entering the vertex, might be defined in a similar way.
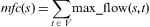
Software
References
- AHUJA, R. K., MAGNANTI, T. L. & ORLIN, J. B. 1993. Network flows: theory, algorithms, and applications.
- KOSCHÜTZKI, D., JUNKER, B. H., SCHWENDER, J. & SCHREIBER, F. 2010. Structural analysis of metabolic networks based on flux centrality. Journal of Theoretical Biology, 265, 261-269.