Eigenvector Centrality
Definition
A measure of importance of nodes in a network using the adjacency and eigenvector matrices.
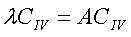where CIV is a eigenvector and λ is an eigenvalue. Only the largest eigenvalue will generate the desired centrality measurement.
It scores the relative importance of all nodes in the network by weighting connections to highly important nodes more than connections to nodes of low importance. As graph G is undirected and loop-free, the adjacency matrix A is symmetric, and all diagonal entries are 0. Eigenvector centrality can be computed by finding the principal eigenvector of the adjacency matrix A. In general, there will be many different eigenvalues λ for which an eigenvector solution exists. However, the additional requirement that all the entries in the eigenvector be positive implies (by the Perron–Frobenius theorem) that only the largest eigenvalue will generate the desired centrality measurement. [ZHANG, A. 2009]
Eigenvector centrality (EC) is not restricted to shortest paths and is defined as the principal or dominant eigenvector of the adjacency matrix A representing the connected subgraph or component of the network. It simulates a mechanism in which each node affects all of its neighbors simultaneously. EC cannot be considered as a measure of centrality whereby nodes are ranked according to their participation in different network subgraphs. For instance, in a graph with all nodes having the same degree (a regular graph), all the components of the main eigenvalue are identical, even if they participate in different subgraphs. EC is better interpreted as a sort of extended degree centrality which is proportional to the sum of the centralities of the node’ neighbors. Consequently, a node has high value of EC either if it is connected to many other nodes or if it is connected to others that themselves have high EC. [RODRÍGUEZ, J. A. 2007]
EC is suited to measure nodes’ power to influence other nodes in the network both directly and indirectly through its neighbors. Connections to neighbors that are in turn well connected themselves are rated higher than connections to neighbors that are weakly connected.
An intuitive process to compute eigenvector centrality is to give every node a starting random positive amount of influence. Each node then splits its influence evenly and divides it amongst its outward neighbors, receiving from its inward neighbors in kind. This process repeats until everyone is giving out as much as they're taking in and the system has reached steady state. The amount of influence they have at this steady state is their eigenvector centrality. Computationally this process is called the power method. We know that this process has converged when the vector of influence changes only by a constant as follows.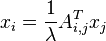
Where xi is the amount of influence that node i carries, Ai,j is the adjacency matrix and λ happens to be the principal eigenvalue.
Google's PageRank is a variant of the Eigenvector centrality measure. Another closely related centrality measure is Katz centrality.
Edge Eigenvector centrality
Bröhl, T. and Lehnertz, K., 2019. Centrality-based identification of important edges in complex networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 29(3), p.033115.
Ruggeri, N. and De Bacco, C., 2019, December. Sampling on Networks: Estimating Eigenvector Centrality on Incomplete Networks. In International Conference on Complex Networks and Their Applications (pp. 90-101). Springer, Cham.
Roddenberry, T.M. and Segarra, S., 2020, May. Blind inference of centrality rankings from graph signals. In ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 5335-5339). IEEE.
Roddenberry, T.M. and Segarra, S., 2020. Blind Estimation of Eigenvector Centrality from Graph Signals: Beyond Low-pass Filtering. arXiv preprint arXiv:2005.00659.
Yin, R.R., Guo, Q., Yang, J.N. and Liu, J.G., 2018. Inter-layer similarity-based eigenvector centrality measures for temporal networks. Physica A: Statistical Mechanics and its Applications, 512, pp.165-173.
Tudisco, F. and Higham, D.J., 2021. Node and Edge Eigenvector Centrality for Hypergraphs. arXiv preprint arXiv:2101.06215.
Sathyakala, M. and Sangeetha, M., 2021. Enhanced Eigenvector Centrality for Real-World Temporal Networks. Journal of Computational and Theoretical Nanoscience, 18(3), pp.1063-1068.
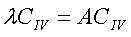
It scores the relative importance of all nodes in the network by weighting connections to highly important nodes more than connections to nodes of low importance. As graph G is undirected and loop-free, the adjacency matrix A is symmetric, and all diagonal entries are 0. Eigenvector centrality can be computed by finding the principal eigenvector of the adjacency matrix A. In general, there will be many different eigenvalues λ for which an eigenvector solution exists. However, the additional requirement that all the entries in the eigenvector be positive implies (by the Perron–Frobenius theorem) that only the largest eigenvalue will generate the desired centrality measurement. [ZHANG, A. 2009]
Eigenvector centrality (EC) is not restricted to shortest paths and is defined as the principal or dominant eigenvector of the adjacency matrix A representing the connected subgraph or component of the network. It simulates a mechanism in which each node affects all of its neighbors simultaneously. EC cannot be considered as a measure of centrality whereby nodes are ranked according to their participation in different network subgraphs. For instance, in a graph with all nodes having the same degree (a regular graph), all the components of the main eigenvalue are identical, even if they participate in different subgraphs. EC is better interpreted as a sort of extended degree centrality which is proportional to the sum of the centralities of the node’ neighbors. Consequently, a node has high value of EC either if it is connected to many other nodes or if it is connected to others that themselves have high EC. [RODRÍGUEZ, J. A. 2007]
EC is suited to measure nodes’ power to influence other nodes in the network both directly and indirectly through its neighbors. Connections to neighbors that are in turn well connected themselves are rated higher than connections to neighbors that are weakly connected.
An intuitive process to compute eigenvector centrality is to give every node a starting random positive amount of influence. Each node then splits its influence evenly and divides it amongst its outward neighbors, receiving from its inward neighbors in kind. This process repeats until everyone is giving out as much as they're taking in and the system has reached steady state. The amount of influence they have at this steady state is their eigenvector centrality. Computationally this process is called the power method. We know that this process has converged when the vector of influence changes only by a constant as follows.
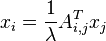
Google's PageRank is a variant of the Eigenvector centrality measure. Another closely related centrality measure is Katz centrality.
Edge Eigenvector centrality
Bröhl, T. and Lehnertz, K., 2019. Centrality-based identification of important edges in complex networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 29(3), p.033115.
Ruggeri, N. and De Bacco, C., 2019, December. Sampling on Networks: Estimating Eigenvector Centrality on Incomplete Networks. In International Conference on Complex Networks and Their Applications (pp. 90-101). Springer, Cham.
Roddenberry, T.M. and Segarra, S., 2020, May. Blind inference of centrality rankings from graph signals. In ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 5335-5339). IEEE.
Roddenberry, T.M. and Segarra, S., 2020. Blind Estimation of Eigenvector Centrality from Graph Signals: Beyond Low-pass Filtering. arXiv preprint arXiv:2005.00659.
Yin, R.R., Guo, Q., Yang, J.N. and Liu, J.G., 2018. Inter-layer similarity-based eigenvector centrality measures for temporal networks. Physica A: Statistical Mechanics and its Applications, 512, pp.165-173.
Tudisco, F. and Higham, D.J., 2021. Node and Edge Eigenvector Centrality for Hypergraphs. arXiv preprint arXiv:2101.06215.
Sathyakala, M. and Sangeetha, M., 2021. Enhanced Eigenvector Centrality for Real-World Temporal Networks. Journal of Computational and Theoretical Nanoscience, 18(3), pp.1063-1068.
Requirements
Require connected and strongly connected network.
Software
- CentiBiN
http://centibin.ipk-gatersleben.de/ - CentiLib
http://centilib.ipk-gatersleben.de/ - CentiScaPe
http://www.cbmc.it/~scardonig/centiscape/centiscape.php - CytoNCA
http://apps.cytoscape.org/apps/cytonca - Functional Genomics Assistant (FUGA)
http://code.google.com/p/fuga - GraphStream
http://graphstream-project.org/ - graph-tool
http://graph-tool.skewed.de/ - igraph
http://igraph.org - JGraphT-sna
https://bitbucket.org/sorend/jgrapht-sna - JUNG
http://jung.sourceforge.net - MultiNet
http://www.sfu.ca/personal/archives/richards/Multinet/Pages/multinet.htm - neo4j
http://neo4j.com/ - NetworKit
https://networkit.iti.kit.edu/ - NetworkX
https://networkx.github.io/ - NodeXL
http://nodexl.codeplex.com/ - Sentinel Visualizer
http://www.fmsasg.com/SocialNetworkAnalysis/ - sna
http://CRAN.R-project.org/package=sna - UCINET
https://sites.google.com/site/ucinetsoftware/ - Visone
http://visone.info/ - Wolfram
http://www.wolfram.com
References
- P. Bonacich. Factoring and weighting approaches to status scores and clique identification. Journal of Mathematical Sociology, 2:113–120, 1972.
- ZHANG, A. 2009. Protein Interaction Networks: Computational Analysis, Cambridge University Press.
- RODRÍGUEZ, J. A., ESTRADA, E. & GUTIÉRREZ, A. 2007. Functional centrality in graphs. Linear and Multilinear Algebra, 55, 293-302.
- CSARDI, G. & NEPUSZ, T. 2006. The igraph software package for complex network research. InterJournal, Complex Systems, 1695. [http://igraph.org]
- JUNG, the Java Universal Network/Graph Framework [http://jung.sourceforge.net]