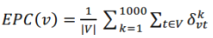EPC - Edge Percolated Component
Definition
For an interaction network G, assign a removing probability p to every edge. Let G' be a realization of the random edge removing from G. If nodes v and w are connected in G', set dvw be 1, otherwise set dvw be 0. The percolated connectivity of v and w, cvw, is defined to be the average of dvw over realizations. The size of percolated component containing node v, sv, is defined to be the sum of cvw over nodes w. The score of node v, EPC(v), is defined to be sv. [LIN, C.-Y. 2008]
cyto-Hubba impelementation:
Given a threshold (0 ≤ the threshold ≤ 1), we create 1000 reduced network by asigning a random number between 0 and 1 to every edge and remove edges if their associated random numbers are less than the threshold.
Let the Gk be the reduced network generated at the kth time reduced process. If nodes u and v are connected in Gk, set σkvt to 1; otherwise σkvt =0. For a node v in G, EPC(v) is defined as:
cyto-Hubba impelementation:
Given a threshold (0 ≤ the threshold ≤ 1), we create 1000 reduced network by asigning a random number between 0 and 1 to every edge and remove edges if their associated random numbers are less than the threshold.
Let the Gk be the reduced network generated at the kth time reduced process. If nodes u and v are connected in Gk, set σkvt to 1; otherwise σkvt =0. For a node v in G, EPC(v) is defined as:
References
- CHEN, S.-H., CHIN, C.-H., WU, H.-H., HO, C.-W., KO, M.-T. & LIN, C.-Y. cyto-Hubba: A Cytoscape plug-in for hub object analysis in network biology. 20th International Conference on Genome Informatics, 2009.
- CHIN, C.-S. & SAMANTA, M. P. 2003. Global snapshot of a protein interaction network—a percolation based approach. Bioinformatics, 19, 2413-2419.
- LIN, C.-Y., CHIN, C.-H., WU, H.-H., CHEN, S.-H., HO, C.-W. & KO, M.-T. 2008. Hubba: hub objects analyzer—a framework of interactome hubs identification for network biology. Nucleic acids research, 36, W438-W443.