DiffSLC Centrality
Definition
The proposed DiffSLC method combines multiple centralities. An investigation in combining multiple centralities to benefit from strengths of each is underexplored.
DiffSLC is aimed at finding essential proteins in a PPI network using graph topological features as well as experimental data.
Based on the results showing success of centrality-lethality principle for PPI networks, DiffSLC uses gene expression data to bias degree centrality towards interacting proteins that have similar expression profiles from a transcript-based context.
DiffSLC exploits the advantages of eigenvector centrality and edge clustering coefficients. Eigenvector centrality provides higher ranks to low-degree nodes that are connected to high degree nodes, while the edge clustering coefficient ranks graph edges based on their involvement in closely connected small subnetworks.
DiffSLC is defined as a weighted combination of the eigenvector centrality and the coexpression-biased degree centrality. While degree centrality is able to capture many of the essential proteins in the top 20% of degree sorted nodes, it also misses several known essential proteins with fewer interactions. Many of these low-degree nodes are connected to other higher degree nodes. Eigenvector centrality (EC) ranks such nodes higher; hence DiffSLC captures additional essential proteins by giving partial weight to nodes ranked highly by EC.
Furthermore, the co-expression bias for each pair of interacting proteins is weighted by the coexpression amount and by the edge-clustering coefficient. The coexpression bias detects interacting proteins that are also highly co-expressed in a given gene expression condition. The edge clustering coefficient (ECC) bias promotes protein interactions that may affect other interactions of its interacting proteins, or be affected by other interactions of its interacting proteins. These contributions are captured here via the β and ω parameters, which vary the levels of contributions from each set of experimental data and centralities.
For the graph G, the DiffSLC of an arbitrary node u can be calculated as follows, where the BDC(u) is the biased degree centrality of a node u.
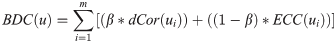where, u has m incident edges, and β ∈ [0, 1].
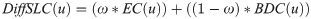where, EC is the eigenvector centrality, and ω ∈ [0, 1].
DiffSLC is defined as a weighted combination of the eigenvector centrality and the coexpression-biased degree centrality. While degree centrality is able to capture many of the essential proteins in the top 20% of degree sorted nodes, it also misses several known essential proteins with fewer interactions. Many of these low-degree nodes are connected to other higher degree nodes. Eigenvector centrality (EC) ranks such nodes higher; hence DiffSLC captures additional essential proteins by giving partial weight to nodes ranked highly by EC.
Furthermore, the co-expression bias for each pair of interacting proteins is weighted by the coexpression amount and by the edge-clustering coefficient. The coexpression bias detects interacting proteins that are also highly co-expressed in a given gene expression condition. The edge clustering coefficient (ECC) bias promotes protein interactions that may affect other interactions of its interacting proteins, or be affected by other interactions of its interacting proteins. These contributions are captured here via the β and ω parameters, which vary the levels of contributions from each set of experimental data and centralities.
For the graph G, the DiffSLC of an arbitrary node u can be calculated as follows, where the BDC(u) is the biased degree centrality of a node u.
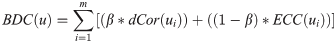
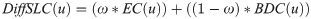
Software
References
- Mistry, D., Wise, R.P. and Dickerson, J.A., 2017. DiffSLC: A graph centrality method to detect essential proteins of a protein-protein interaction network. PLOS ONE, 12(11), p.e0187091.
DOI: 10.1371/journal.pone.0187091
