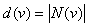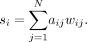Degree Centrality
Definition
Number of direct neighbors of node v
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph.
Degree centrality is a local and static metric, since it considers only the directly connected neighbors of a vertex in a static state. Nonetheless, it serves as a useful indicator of the extent of attachment of a vertex to the graph. [ZHANG, A. 2009]
In degree/Out degree
In directed networks two variants of the degree centrality may be appropriate: the in-degree centrality ciD(v) = d−(v) and the out-degree centrality coD(v) = d+(v). [BRANDES, U. 2005]
Degree Weighted
A more significant measure of the network properties in terms of the actual weights is obtained by extending the definition of vertex degree ki = Σjaij in terms of the vertex strength si, defined as Formula
In biological terms
The degree allows an immediate evaluation of the regulatory relevance of the node. For instance, in signaling networks, proteins with very high degree are interacting with several other signaling proteins, thus suggesting a central regulatory role, that is they are likely to be regulatory hubs. For instance, signaling proteins encoded by oncogenes, such as HRAS, SRC or TP53, are hubs. De- pending on the nature of the protein, the degree could indicate a central role in amplification (kinases), diversification and turnover (small GTPases), signaling module assembly (docking proteins), gene expression (transcription factors), etc. Signaling networks have typically a scale-free architecture. [SCARDONI, G.]
Degree centrality can be interpreted as a measure of immediate influence, as opposed to long-term effect in the network. For instance, if a certain proportion of nodes in the network are infected, those nodes having a direct connection with them will also be infected. However, although a node in a network may be linked to only one node, the risk of infection to the first node remains high if the latter is connected to many others. [RODRÍGUEZ, J. A. 2007]
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph.
Degree centrality is a local and static metric, since it considers only the directly connected neighbors of a vertex in a static state. Nonetheless, it serves as a useful indicator of the extent of attachment of a vertex to the graph. [ZHANG, A. 2009]
In degree/Out degree
In directed networks two variants of the degree centrality may be appropriate: the in-degree centrality ciD(v) = d−(v) and the out-degree centrality coD(v) = d+(v). [BRANDES, U. 2005]
Degree Weighted
A more significant measure of the network properties in terms of the actual weights is obtained by extending the definition of vertex degree ki = Σjaij in terms of the vertex strength si, defined as Formula
In biological terms
The degree allows an immediate evaluation of the regulatory relevance of the node. For instance, in signaling networks, proteins with very high degree are interacting with several other signaling proteins, thus suggesting a central regulatory role, that is they are likely to be regulatory hubs. For instance, signaling proteins encoded by oncogenes, such as HRAS, SRC or TP53, are hubs. De- pending on the nature of the protein, the degree could indicate a central role in amplification (kinases), diversification and turnover (small GTPases), signaling module assembly (docking proteins), gene expression (transcription factors), etc. Signaling networks have typically a scale-free architecture. [SCARDONI, G.]
Degree centrality can be interpreted as a measure of immediate influence, as opposed to long-term effect in the network. For instance, if a certain proportion of nodes in the network are infected, those nodes having a direct connection with them will also be infected. However, although a node in a network may be linked to only one node, the risk of infection to the first node remains high if the latter is connected to many others. [RODRÍGUEZ, J. A. 2007]
Software
- AllegroGraph
http://franz.com/agraph/allegrograph/ - CentiBiN
http://centibin.ipk-gatersleben.de/ - CentiLib
http://centilib.ipk-gatersleben.de/ - cyto-Hubba
http://hub.iis.sinica.edu.tw/cytohubba/ - CytoNCA
http://apps.cytoscape.org/apps/cytonca - EgoNet
http://escoladeredes.net/profiles/blogs/egonet-1 - Functional Genomics Assistant (FUGA)
http://code.google.com/p/fuga - GraphStream
http://graphstream-project.org/ - igraph
http://igraph.org - JGraphT-sna
https://bitbucket.org/sorend/jgrapht-sna - JUNG
http://jung.sourceforge.net - MultiNet
http://www.sfu.ca/personal/archives/richards/Multinet/Pages/multinet.htm - NetVis Module
http://www.netvis.org/ Module
- NetworkAnalyzer
http://med.bioinf.mpi-inf.mpg.de/networkanalyzer/ - NetworKit
https://networkit.iti.kit.edu/ - NetworkX
https://networkx.github.io/ - NodeXL
http://nodexl.codeplex.com/ - Pajek
http://pajek.imfm.si/ - qgraph
http://sachaepskamp.com/qgraph - SBEToolbox
https://github.com/biocoder/SBEToolbox/releases - Sentinel Visualizer
http://www.fmsasg.com/SocialNetworkAnalysis/ - sna
http://CRAN.R-project.org/package=sna - SocNetV
http://socnetv.sourceforge.net/ - tnet
http://cran.r-project.org/web/packages/tnet/ - UCINET
https://sites.google.com/site/ucinetsoftware/ - Visone
http://visone.info/ - Wolfram
http://www.wolfram.com
References
- Proctor, C.H. and Loomis, C.P., 1951. Analysis of sociometric data. Research methods in social relations, 2, pp.561-85.
- A HAGBERG, D. S., P SWART. Exploring Network Structure, Dynamics, and Function using NetworkX. In: G VAROQUAUX, T. V., J MILLMAN, ed. Proceedings of the 7th Python in Science conference (SciPy 2008), 2008. 11-15.
- BARRAT, A., BARTHÉLEMY, M., PASTOR-SATORRAS, R. & VESPIGNANI, A. 2004. The architecture of complex weighted networks. Proceedings of the National Academy of Sciences of the United States of America, 101, 3747-3752.
- BRANDES, U. & ERLEBACH, T. 2005. Network Analysis: Methodological Foundations, U.S. Government Printing Office.
- CSARDI, G. & NEPUSZ, T. 2006. The igraph software package for complex network research. InterJournal, Complex Systems, 1695. [http://igraph.org]
- GRÄßLER, J., KOSCHÜTZKI, D. & SCHREIBER, F. 2012. CentiLib: comprehensive analysis and exploration of network centralities. Bioinformatics, 28, 1178-1179.
- JUNG, the Java Universal Network/Graph Framework [http://jung.sourceforge.net]
- JUNKER, B. H., KOSCHÜTZKI, D. & SCHREIBER, F. 2006. Exploration of biological network centralities with CentiBiN. BMC bioinformatics, 7, 219.
- LIN, C.-Y., CHIN, C.-H., WU, H.-H., CHEN, S.-H., HO, C.-W. & KO, M.-T. 2008. Hubba: hub objects analyzer—a framework of interactome hubs identification for network biology. Nucleic acids research, 36, W438-W443.
- RODRÍGUEZ, J. A., ESTRADA, E. & GUTIÉRREZ, A. 2007. Functional centrality in graphs. Linear and Multilinear Algebra, 55, 293-302.
- SCARDONI, G., LAUDANNA, C., TOSADORI, G., FABBRI, F. & FAIZAAN, M. CentiScaPe: Network centralities for Cytoscape. http://www.cbmc.it/~scardonig/centiscape/CentiScaPefiles/CentralitiesTutorial.pdf
- SCARDONI, G., PETTERLINI, M. & LAUDANNA, C. 2009. Analyzing biological network parameters with CentiScaPe. Bioinformatics, 25, 2857-2859.
DOI: 10.1093/bioinformatics/btp517


- ZHANG, A. 2009. Protein Interaction Networks: Computational Analysis, Cambridge University Press.