Coreness Centrality
Definition
The coreness centrality, which is estimated with the k-shell indices
of the neighbors that are adjacent to a spreader, is a simple but notably powerful indicator to assess the capability of
information dissemination through the network. This approach is to consider both the degree and the coreness of a node
coincidently by counting the k-shell indices of its neighbor or neighbor of neighbors.
The basic assumption is that a spreader with more connections to the neighbors located in the core of the network is more powerful. Based on this assumption, the neighborhood coreness Cnc of node v is defined as: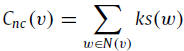 where N(v) is the set of the neighbors adjacent to node v and ks(w) is the k-shell index of its neighbor node w. Recursively,
the extended neighborhood coreness Cnc+ of node v is defined as follows:
where N(v) is the set of the neighbors adjacent to node v and ks(w) is the k-shell index of its neighbor node w. Recursively,
the extended neighborhood coreness Cnc+ of node v is defined as follows:
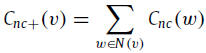 where Cnc(w) is the neighborhood coreness of neighbor w of node v.
This observation implies that the extended
coreness Cnc+ gives more weights to the coreness than does the neighborhood coreness Cnc.
where Cnc(w) is the neighborhood coreness of neighbor w of node v.
This observation implies that the extended
coreness Cnc+ gives more weights to the coreness than does the neighborhood coreness Cnc.
Once the k-shell index is provided by decomposing the network globally, the coreness centrality can be obtained as a local measure. This feature is significant when we analyze notably large networks or highly dynamic networks.
The basic assumption is that a spreader with more connections to the neighbors located in the core of the network is more powerful. Based on this assumption, the neighborhood coreness Cnc of node v is defined as:
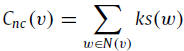
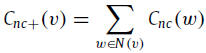
Once the k-shell index is provided by decomposing the network globally, the coreness centrality can be obtained as a local measure. This feature is significant when we analyze notably large networks or highly dynamic networks.
Requirements
Unweighted, undirected, and simple networks.
Computational complexity
O(m)
where m is the number of edges in the network.
where m is the number of edges in the network.
Software
References
- BAE, J. & KIM, S. 2014. Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Physica A: Statistical Mechanics and its Applications, 395, 549-559.
DOI: 10.1016/j.physa.2013.10.047

