Composite Centrality
Definition
The composite centrality is a measure for general weighted and directed complex networks, based
on measure standardisation and invariant statistical inheritance schemes. Different schemes generate different
intermediate abstract measures providing additional information, while the composite centrality
measure tends to the standard normal distribution. This offers a unified scale to measure node and edge
centralities for complex evolving networks under a uniform framework.
By only using standardised measures (SM), it is straightforward to construct arbitrary composite measures. Having two node measures, A and B, for which ¯A and ¯B denote the corresponding SM, the composite centrality measure is defined by the statistically normalised measure of the sum of the two measures via value-byvalue addition. One has: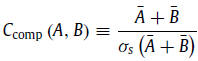 where σs(·) stands for the sample standard deviation. Ccomp is
a new SM carrying an abstract physical meaning depending on
the original measures. From here on, standardised measures are
denoted with a bar. Having a set of n measures, M ∋ Mi, i ∈
{1, . . . , n}, a generalisation of above takes the form
where σs(·) stands for the sample standard deviation. Ccomp is
a new SM carrying an abstract physical meaning depending on
the original measures. From here on, standardised measures are
denoted with a bar. Having a set of n measures, M ∋ Mi, i ∈
{1, . . . , n}, a generalisation of above takes the form
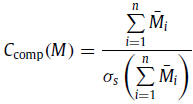
By only using standardised measures (SM), it is straightforward to construct arbitrary composite measures. Having two node measures, A and B, for which ¯A and ¯B denote the corresponding SM, the composite centrality measure is defined by the statistically normalised measure of the sum of the two measures via value-byvalue addition. One has:
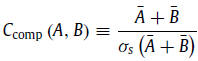
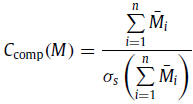
Software
References
- JOSEPH, A. C. & CHEN, G. 2014. Composite centrality: A natural scale for complex evolving networks. Physica D: Nonlinear Phenomena, 267, 58-67.