Communicability Betweenness Centrality
Definition
Communicability betweenness measure makes use of the number of walks connecting every pair of nodes as the basis of a betweenness centrality measure.
Let G=(V,E) be a simple undirected graph with n nodes and m edges, and A denote the adjacency matrix of G.
Let G(r)=(V,E(r)) be the graph resulting from removing all edges connected to node r but not the node itself.
The adjacency matrix for G(r) is A+E(r), where E(r) has nonzeros only in row and column r.
The communicability betweenness of a node r is: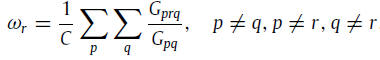 where Gprq=(eA)pq−(eA+E(r))pq is the number of walks involving node r, Gpq=(eA)pq is the number of closed walks starting at node p and ending at node q, and C=(n−1)2−(n−1) is a normalization factor equal to the number of terms in the sum.
where Gprq=(eA)pq−(eA+E(r))pq is the number of walks involving node r, Gpq=(eA)pq is the number of closed walks starting at node p and ending at node q, and C=(n−1)2−(n−1) is a normalization factor equal to the number of terms in the sum.
The resulting ωr takes values between zero and one. The lower bound cannot be attained for a connected graph, and the upper bound is attained in the star graph.
Let G=(V,E) be a simple undirected graph with n nodes and m edges, and A denote the adjacency matrix of G.
Let G(r)=(V,E(r)) be the graph resulting from removing all edges connected to node r but not the node itself.
The adjacency matrix for G(r) is A+E(r), where E(r) has nonzeros only in row and column r.
The communicability betweenness of a node r is:
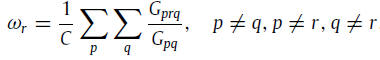
The resulting ωr takes values between zero and one. The lower bound cannot be attained for a connected graph, and the upper bound is attained in the star graph.
Software
References
- A HAGBERG, D. S., P SWART. Exploring Network Structure, Dynamics, and Function using NetworkX. In: G VAROQUAUX, T. V., J MILLMAN, ed. Proceedings of the 7th Python in Science conference (SciPy 2008), 2008. 11-15.
- ESTRADA, E., HIGHAM, D. J. & HATANO, N. 2009. Communicability betweenness in complex networks. Physica A: Statistical Mechanics and its Applications, 388, 764-774.
DOI: 10.1016/j.physa.2008.11.011


Comments
I know your explanation for the mathematical definition of this measure starts with "Let G=(V,E) be a simple undirected graph...", nevertheless I would like to ask if this centrality measure, along with your algorithm ("communibet" in package centiserve) can be used in directed weighted networks. Many thanks! |
|
| Add Replay | written July 29, 2021, 11:57 am by Anonymous User |