Bridging Centrality
Definition
A bridge is a node or an edge that is located between and connects modules in a graph. In other words, a bridge is a node v or an edge e that has high bridging centrality value.
To obtain a metric capable of identifying bridges, The idea that the number of edges entering or leaving the direct neighbor subgraph of a node v relative to the number of edges remaining within the direct neighbor subgraph of a node v is high at bridges is used to formulate the concept of bridging coefficient for both nodes and edges.
The bridging coefficient of a node v is defined as the average probability of leaving the direct neighbor subgraph of a node v. The bridging coefficient of a node v is defined by: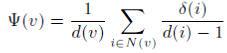
where d(v) is the degree of a node v and Σ(v) is the number of edges leaving the direct neighbor subgraph of node v among the edges incident to each direct neighbor node i of node v.
The bridging coefficient of an edge e is defined as the product of weighted average of bridging coefficient of two incident nodes i and j for an edge e and the reciprocal of the number of common direct neighbor nodes of nodes i and j. The bridging coefficient of an edge e is defined by: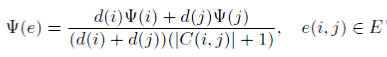
where nodes i and j are the two incident nodes to edge e, d(i) is the degree of a node i, Ψ(i) is the bridging coefficient of node i, C(i, j) is the set of common direct neighbor nodes of nodes i and j.
The rank product [BREITLING, R., 2004] which is defined as the product of rank of the betweeness and the rank of the bridging coefficient used for computing the bridging centrality. This normalization procedure corrects for the differences in scale between the betweeness and the bridging coefficient.
The bridging centrality of a node v is defined by: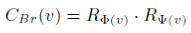
where RΦ(v) is the rank of a node v in betweenness and RΨ(v) is the rank of a node v in bridging coefficient.
In rank product normalization, nodes in a graph are ordered by scores measured for each metric, e.g., bridging coefficient and betweenness. Then, we take the rankings of a node v in the sorted order for each metric and bridging centrality uses the product of the rankings in each metric for a node v.
The bridging centrality of an edge e is defined by: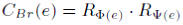
where RΦ(e) is the rank of an edge e in betweenness and is the rank of an edge e in bridging coefficient.
In above formulas, the first term, which measures global importance of a node or an edge, represents the fraction of shortest paths passing through a node or an edge. The second term measures the local topological property around a node or an edge, i.e., the probability of leaving the direct neighbor subgraph of a node or an edge. A bridge is a node v or an edge e that has high bridging centrality value relative to other nodes or edges on the same graph.
Based on these definitions, the bridging centrality is capable of identifying nodes or edges that are located and connect subregions of the network and are therefore potential bottlenecks to information flow between modules [HWANG, W., 2008].
The bridging coefficient of a node determines the extent how well the node is located between high degree nodes. It assesses the local bridging characteristics in the neighborhood. Intuitively, there should be more congestion on the smaller degree node since the smaller degree nodes have lesser number of outlets than the bigger degree nodes have. So if we consider the reciprocal of the degree of a node as the "resistance" of the node, the bridging coefficient can be viewed as the ratio of the resistance of a node to the sum of the resistance of its neighbours.
In Biological Terms
Bridging centrality can be used to break up modules in a network for clustering purpose. Functional modules or physical modules in biological networks can be detected using the bridging nodes chosen by bridging centrality. Second, it can be use to identigy the most critical points interrupting the information flow in a network, for network protection and robustness improvement purposes. Third, in biological application, bridging centrality can be used to locate the key proteins, which are the connecting nodes among functional modules. [SCARDONI, G.]
To obtain a metric capable of identifying bridges, The idea that the number of edges entering or leaving the direct neighbor subgraph of a node v relative to the number of edges remaining within the direct neighbor subgraph of a node v is high at bridges is used to formulate the concept of bridging coefficient for both nodes and edges.
The bridging coefficient of a node v is defined as the average probability of leaving the direct neighbor subgraph of a node v. The bridging coefficient of a node v is defined by:
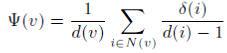
The bridging coefficient of an edge e is defined as the product of weighted average of bridging coefficient of two incident nodes i and j for an edge e and the reciprocal of the number of common direct neighbor nodes of nodes i and j. The bridging coefficient of an edge e is defined by:
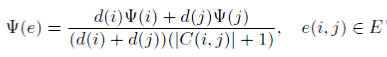
The rank product [BREITLING, R., 2004] which is defined as the product of rank of the betweeness and the rank of the bridging coefficient used for computing the bridging centrality. This normalization procedure corrects for the differences in scale between the betweeness and the bridging coefficient.
The bridging centrality of a node v is defined by:
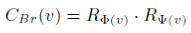
In rank product normalization, nodes in a graph are ordered by scores measured for each metric, e.g., bridging coefficient and betweenness. Then, we take the rankings of a node v in the sorted order for each metric and bridging centrality uses the product of the rankings in each metric for a node v.
The bridging centrality of an edge e is defined by:
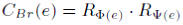
In above formulas, the first term, which measures global importance of a node or an edge, represents the fraction of shortest paths passing through a node or an edge. The second term measures the local topological property around a node or an edge, i.e., the probability of leaving the direct neighbor subgraph of a node or an edge. A bridge is a node v or an edge e that has high bridging centrality value relative to other nodes or edges on the same graph.
Based on these definitions, the bridging centrality is capable of identifying nodes or edges that are located and connect subregions of the network and are therefore potential bottlenecks to information flow between modules [HWANG, W., 2008].
The bridging coefficient of a node determines the extent how well the node is located between high degree nodes. It assesses the local bridging characteristics in the neighborhood. Intuitively, there should be more congestion on the smaller degree node since the smaller degree nodes have lesser number of outlets than the bigger degree nodes have. So if we consider the reciprocal of the degree of a node as the "resistance" of the node, the bridging coefficient can be viewed as the ratio of the resistance of a node to the sum of the resistance of its neighbours.
In Biological Terms
Bridging centrality can be used to break up modules in a network for clustering purpose. Functional modules or physical modules in biological networks can be detected using the bridging nodes chosen by bridging centrality. Second, it can be use to identigy the most critical points interrupting the information flow in a network, for network protection and robustness improvement purposes. Third, in biological application, bridging centrality can be used to locate the key proteins, which are the connecting nodes among functional modules. [SCARDONI, G.]
Baruah, A.K. and Bora, T., 2018. Bridging centrality: Identifying bridging nodes in transportation network. International Journal of Advanced Networking and Applications, 9(6), pp.3669-3673.
Software
References
- BREITLING, R., ARMENGAUD, P., AMTMANN, A. & HERZYK, P. 2004. Rank products: a simple, yet powerful, new method to detect differentially regulated genes in replicated microarray experiments. FEBS letters, 573, 83-92.
- HWANG, W., KIM, T., RAMANATHAN, M. & ZHANG, A. Bridging centrality: graph mining from element level to group level. Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining, 2008. ACM, 336-344.
- HWANG, W., ZHANG, A. & RAMANATHAN, M. 2008. Identification of information flow-modulating drug targets: a novel bridging paradigm for drug discovery. Clinical Pharmacology & Therapeutics, 84, 563-572.
- SCARDONI, G., LAUDANNA, C., TOSADORI, G., FABBRI, F. & FAIZAAN, M. CentiScaPe: Network centralities for Cytoscape. http://www.cbmc.it/~scardonig/centiscape/CentiScaPefiles/CentralitiesTutorial.pdf
- SCARDONI, G., PETTERLINI, M. & LAUDANNA, C. 2009. Analyzing biological network parameters with CentiScaPe. Bioinformatics, 25, 2857-2859.
DOI: 10.1093/bioinformatics/btp517
